通貨を取引していると、
なんとなくこの通貨はボラティリティ（変動幅）が大きいな、
ということはよく感じると思います。

しかし、ボラティリティが小さい通貨同士で、
どちらがよりボラティリティが小さいか？
というように、細かいところまで考えると、
ちょっと感覚ではわからないですよね？

ここでは、そのボラティリティを数字で確認する方法を書きたいと思います。

この計算をすれば各通貨のボラティリティが数字で確認できるので、
金利を考慮してどの通貨をレバレッジ何倍で持てば、
一番効率よくリターンが期待できるのか？
というようなこともわかります。

こういった金融工学の計算には、
エクセルが非常に役立ちます。

ではエクセルを使って、
USD/JPYとZAR/JPYのボラティリティを算出して比較してみます。

１．データの取得

まず、以下のサイトから日付を指定して、
USD/JPYとZAR/JPYのデータを取得します。
http://www.oanda.com/convert/fxhistory

日付は「月/日/年」となっているので、
2003年11月22日から2006年11月22日までのデータを取得する場合、

Starting Date:11/22/03
Ending Date:11/22/06

と入力し、Currency Code:に取得する通貨をそれぞれ入力します。

Formatは自分がデータを編集しやすい形式で取得してください。

これをエクセルに貼り付けます。

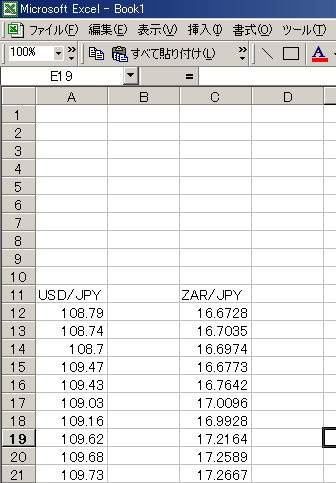
データを取得する期間は1年でもいいのですが、
基本的に長い期間を取得した方がより正確なボラティリティが得られます。

今回は3年分を取得しています。

２．前日比を算出する

ここから全てのデータに対して、 前日比を計算します。

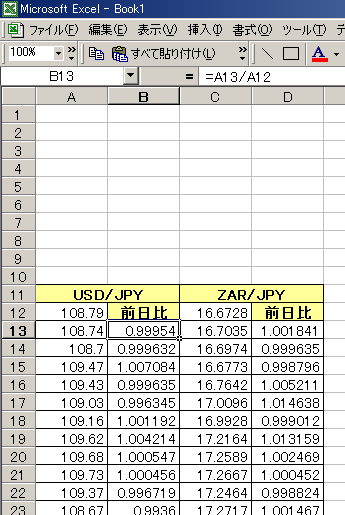
この図では下に行くほどデータが新しいので、
A13/A12という風にして、これをコピーします。

３．標準偏差を算出する

エクセルのSTDEVP関数を使って、
標準偏差を算出します。

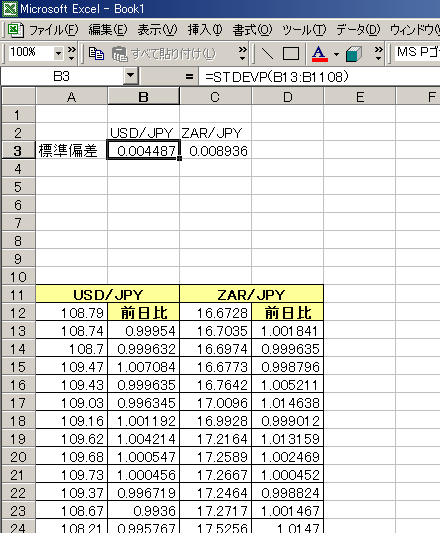
これをパーセント表示に設定すれば、
1日あたりの標準偏差が算出されます。

しかし、金利は年利で計算するのが普通なので、
標準偏差も1年あたりのものに変換します。

通常統計学では、年間の営業日には250日を使います。

理論的には「1日あたりの標準偏差×250日の平方根」
となるので、STDEVP(B13:B1108)*SQRT(250)
とします。

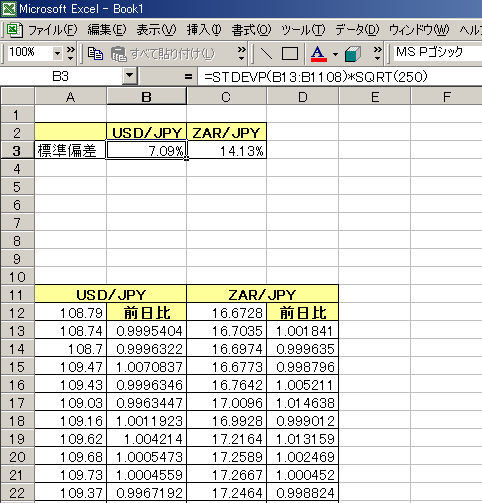
以上でボラティリティの算出は完了です。

こうして算出した標準偏差がそのままボラティリティになります。

これを、ヒストリカルボラティリティと言います。

今回算出したヒストリカルボラティリティは、
たとえばUSD/JPYなら、
年間±7.09%の範囲内に68.3%の確率でおさまる、
ということを意味します。

68.3%の確率で収まるのはそう決まっていると覚えておいてください。

USD/JPYが、ヒストリカルボラティリティの2倍である、
±14.18%の範囲内におさまる確率は95.4%となります。

これは為替に限らず、
どんなデータを対象にしても同じ確率になります。

今回の計算によって、ZAR/JPYのボラティリティは、
USD/JPYのボラティリティのほぼ2倍あるということが確認できます。

スワップ派にとっては、
ヒストリカルボラティリティが小さくスワップ金利が大きい通貨を選べばいい、
ということになります。

また、このヒストリカルボラティリティは、
過去のデータをもとに未来のボラティリティを予測したものです。

したがって、必ず今後もこのボラティリティになるということではありません。

歴史上起こり得なかった突発的な出来事が起これば、
統計学上では起こりえない変動幅になる可能性もあります。